Week 6: In-Class

Coding Practice

Code 6.1: Stable Measurements

An experiment is conducted to measure the growth of microorganisms. The measuring equipment produces unstable values at the beginning of the experiment, so the dataset must be split into two parts: an unstable interval and a stable interval.

Your task is to remove the unstable measurements and keep only the stable interval.

The stable interval begins with the first measurement that is strictly larger than all previous measurements, and strictly smaller than all later measurements.

The first or the last measurement in the dataset cannot be the start of the stable interval. You can assume that at least three measurements are always taken.

Pen & Paper

Consider the sequence 4.3, 5.7, 5.1, 6.4, 7.9, 12.8 shown in the illustration.

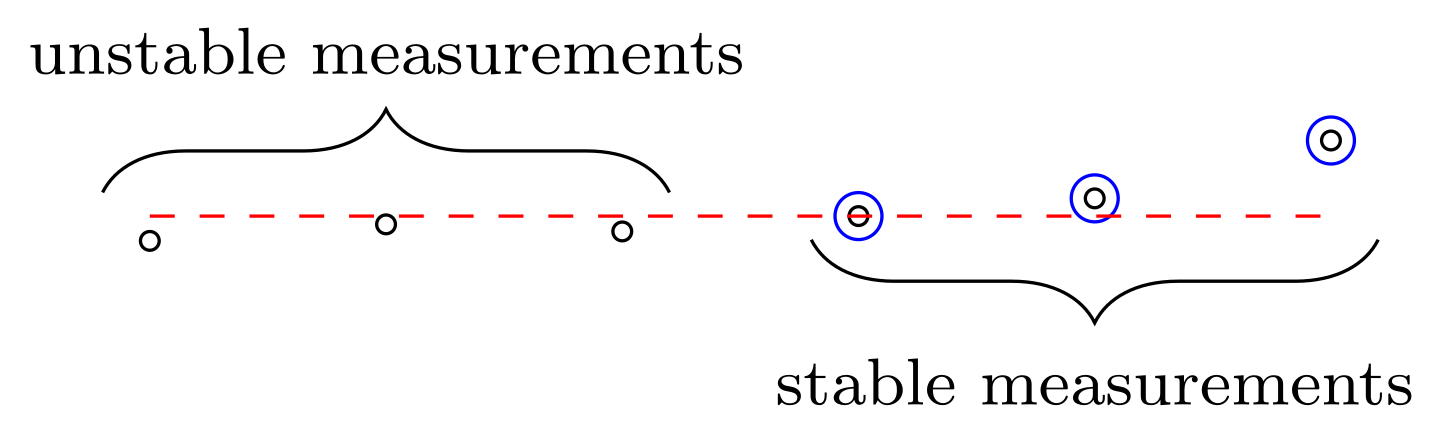
Confirm that the stable measurement for this example are 6.4, 7.9, 12.8.

Based on this example, determine the stable measurements for the following sequences:

• 1.8, 1.9, 1.2, 0.3, 0.2, 1.1, 2.8, 5.0, 9.5, 22.5

• 1.9, 0.3, 0.7, 2.0, 0.6, 0.9, 3.1, 3.7, 8.4

• 1.1, 0.7, 1.4, 0.5

• 0.6, 0.4, 2.2, 1.5, 1.4, 4.0, 4.6, 5.2, 9.0

• 2.0, 0.6, 1.6, 3.6, 3.0, 4.1, 6.9, 7.1, 8.3, 11.9, 13.1, 14.5, 18.7, 20.9, 22.5

• 1.6, 2.7, 5.9, 8.5, 14.2, 18.2, 26.3, 32.1

• 3.0, 1.6, 3.8, 2.7, 4.7, 4.0, 5.4, 5.2, 6.2

• 2.9, 4.7, 4.9, 7.1, 6.9, 9.5, 9.0, 11.8

Demo

Create a function stable_measurements which takes a list with all measurements as input, and returns a list with only stable measurements. If the stable interval is not found (for example, if all measurements are equal), an empty list is to be returned.

Code 6.2: State Durations

Air conditioning system has three states: off (code 0), heating (code 1), and cooling (code 2). Every time the state changes, the system logs the code of the new state and a timestamp measuring the number of seconds since the beginning of the log.

The states are logged in one sequence, and the timestamps in another sequence. We are interested in finding out how long the system has been in each state.

For example consider states 1, 0, 1, 2, 1, 0 with timestamps 0, 405, 515, 825, 2430, 3060.

The system started in heating mode (code 1) at time 0, switched to off (code 0) at time 405, switched back to heating (code 1) at time 515, switched to cooling (code 2) at time 825, switched back to heating (code 1) at time 2430, and finally switched to off (code 0) at time 3060.

Pen & Paper

For the example above, determine how long the system has been in each state.

Then work out the total duration of each state for the following sequences of states and timestamps:

• States 1, 2, 0, timestamps: 0, 243, 565.

• States 2, 1, 2, 0, timestamps: 0, 300, 900, 1000.

• States: 1, 2, 1, 2, 0, timestamps: 0, 200, 500, 600, 800.

Demo

Write a function state_durations that takes as input the list states and the list with timestamps. The function should return a list with three elements: the total duration of state 0, the total duration of state 1, and the total duration of state 2.

Code 6.3: Your Name

Define a list containing your first, last, and any middle names. For example:

my_name = ["Lars", "Løkke", "Rasmussen"]

Now, print out a message like this, but for your name, using the list you defined:

My first name is Lars and my last name is Rasmussen
In total, I have 3 names.

Ensure that your message works for other names, with a varying number of middle names. Test with the my_name defined above and with a person who has no middle name.

Code 6.4: Powers of 2

Define an integer variable n. Now create a list containing the first n powers of \(2\) starting with \(2^1\). For example, for n = 4, the list should contain the values \(2^1, 2^2, 2^3, 2^4\), so that the list is [2, 4, 8, 16] .

Test your code with n = 1, n = 4, and n = 10.

Hint

Start by making an empty list, then use a loop where iterator variable \(i\) takes values from \(1\) to \(n\), and add \(2^i\) to the end of the list in each iteration.

Code 6.5: Average of a List

Write a function average that takes a list of numbers as input and returns the average of the numbers in the list. Test it with the list from the previous exercise for n = 4.

>>> average([2, 4, 8, 16])
7.5

Hint

Instead of traversing the list to add the numbers, you can use the built-in functions sum and len to compute the average.

Code 6.6: Slicing the Months

You are given the following list:

months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']

Use list slicing to extract the following lists from months. Each can be extracted with a single slice:

• spring: The list containing 'Mar' , 'Apr' , and 'May' .

• summer: The list containing 'Jun' , 'Jul' , and 'Aug' .

• quarter_starts: The list containing 'Jan' , 'Apr' , 'Jul' , and 'Oct' (every third month starting from January).

• quarter_ends: The list containing 'Mar' , 'Jun' , 'Sep' , and 'Dec' (every third month starting from March).

• reversed_months: The list containing the months in reverse order.

Now assign the variable winter containing 'Dec' , 'Jan' , 'Feb' . For this, you will need more than just slicing.

Code 6.7: Long Months

Use the months list from the previous exercise along with the following list, which contains the number of days in each month:

days = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]

Define a variable d containing an integer number of days, and set it initially to 30.

Given months, days, and d create a new list, long_months, containing the names of all months that have more than d days. For example, for d = 30, the list should contain:

['Jan', 'Mar', 'May', 'Jul', 'Aug', 'Oct', 'Dec']

Try it also for d = 31 and confirm that the list is empty. Confirm that the result is correct for d = 28 and d = 29.

Code 6.8: How Many Josh?

You are given the following list:

names = ['James', 'Julie', 'Josh', 'John', 'Josh', 'Jill', 'Josh', 'Jenny', 'Josh']

Write a single line of code (using a list method) to find out how many times the string 'Josh' appears in this list.

Code 6.9: Top k Elements

Create a function top_k that takes a list and an integer k as input. It should return a list containing the k largest elements from the list, in ascending order. You can assume the list has k or more elements. Here are examples of using the function:

>>> top_k([0, -5, 2], 1)
[2]
>>> top_k([6, 6, 2, 25, 1, 999, -5], 3)
[6, 25, 999]

Hint

You need to sort the list and then return the last k elements.

After this, modify your function so that the returned list has the items in descending order.

Code 6.10: Is Available?

You are given the following list with the food items available:

menu = ["pasta", "pizza", "salad", "soup", "steak", "chicken", "sandwich"]

Assume you have a variable dish containing the name of a dish you want to order.

Write code that given menu and dish, assigns the variable is_available to True if it’s possible to order the dish at this restaurant, or False if it’s not. For example, given dish = "pasta" should evaluate is_available to True, and dish = "burger" should give False.

Now, write a function which_available that takes two lists, menu and desired_dishes, and returns a list of booleans indicating which of the desired dishes are available. For example:

>>> menu = ["pasta", "pizza", "salad", "soup", "steak", "chicken", "sandwich"]
>>> dishes = ["salad", "beer", "pasta", "hotdog", "dog"]
>>> which_available(menu, dishes)
[True, False, True, False, False]
>>> which_available([], ["salad"])
[False]

Hint

Use the in operator to check if a dish is in the menu. Use looping to check each dish.

Problem Solving

Problem 6.11: Unique Values

Write a function unique_values that takes as input a list and returns a new list that only contains unique values. That is, each item only appears once in the returned list. The elements in the returned list should be in the order they first occur in the input list. You should not modify the input list.

Here are a few examples of using the function:

>>> RNA = ['A', 'G', 'G', 'C', 'U', 'U', 'A', 'A', 'U', 'C', 'C', 'G']
>>> unique_values(RNA)
['A', 'G', 'C', 'U']
>>> RNA # check that the original list is not changed
['A', 'G', 'G', 'C', 'U', 'U', 'A', 'A', 'U', 'C', 'C', 'G']
>>> unique_values(['Fr', 'Fr', 'Sa', 'Su', 'Sa', 'Sa', 'Su', 'Su', 'Mo', 'Fr', 'Sa', 'Fr'])
['Fr', 'Sa', 'Su', 'Mo']
>>> unique_values([1, 2, 20, 6, 210, 20, 2])
[1, 2, 20, 6, 210]

The function should have the following specification:

unique_values.py

unique_values(input_list)

Returns a list of unique values from the input list.

Parameters:

input_list

list

The list from which to extract unique values.

Returns:

list	The unique values from the input list, in the order they first appear.

Problem 6.12: Best Buy

A shopper is given a sum of money and a shopping list. They will start at the top of the list, and will be buying items one by one as long as they have enough money to buy the next item. When they do not have enough money to buy the next item, they will go home.

Write a function which takes a list containing prices of the items on the shopping list and a number representing the sum of money the shopper is given as input. The function should return the total number of items bought by the shopper, before they returned home.

Consider the following example:

>>> best_buy([5, 4, 6, 2, 9, 1, 1, 4], 16)
3

After three bought items the shopper has spent 5 + 4 + 6 = 15 money and has 16 − 15 = 1 money left, which is not enough to buy the next item on the list which costs 2 money. He returns home with three items, and the function should therefore return 3.

The filename and requirements are:

best_buy.py

best_buy(prices, budget)

Calculate the number of items that can be bought with the budget.

Parameters:

prices	list of int	Prices of items in the store.
budget	int	The total budget available to spend.

Returns:

int	The number of items bought.

Problem 6.13: Strategic Buy

Given a list of prices, you developed a strategy for shopping. You want to buy as many items as possible without exceeding your budget. The strategy is to buy the cheapest items first (if you can afford it), then buy second cheapest item (if you can afford it), and keep selecting the next cheapest item until you run out of money.

Write a function which implements this strategy. The function gets two inputs: a list of prices of items in the store, and your budget. The function should return the total number of items bought by the shopper.

Here is an example of using the function:

>>> strategic_buy([1, 3, 2, 5, 4], 7)
3

Try to test the function with test_strategic_buy.py.

The function should have the following specification:

strategic_buy.py

strategic_buy(prices, budget)

Determine the maximum number of items that can be bought with a given budget.

Parameters:

prices	list of int	Prices of items in the store.
budget	int	The total budget available to spend.

Returns:

int	The maximum number of items that can be bought without exceeding the budget.

Problem 6.14: Duplicate Elements

Write a function duplicate_elements that takes a list and an integer and returns a new list with each element repeated dup times sequentially.

Here is an example of using the function:

>>> duplicate_elements([4, "B", 3.9], 3)
[4, 4, 4, 'B', 'B', 'B', 3.9, 3.9, 3.9]

The function should have the following specification:

duplicate_elements.py

duplicate_elements(elements, dup)

Duplicate each element in the list dup times.

Parameters:

elements	list	The list of elements to duplicate.
dup	int	The number of times to duplicate each element.

Returns:

list	The list with each element duplicated dup times.

Problem 6.15: Water Height

The height of the water in a pond changes daily, governed by two factors: the constant decrease in height due to the water outflow and the variable increase in height due to the rain. Given the water height for one day and the rain value, the water height for the next day can be computed as:

\[ h_{\text{today}} = h_{\text{yesterday}} + r - 2 \]

where \(h_{\text{today}}\) is the water height today, \(h_{\text{yesterday}}\) is the water height yesterday, and \(r\) is the rainfall for that day. The water height cannot be negative, so if the computed value is negative, the water height is set to zero.

Write a function water_height that takes as input an integer that describes the initial water height and a list of numbers representing the rainfall for each day, and returns the water height on the final day. Consider the following examples:

>>> water_height(0, [1])
0
>>> water_height(0, [4, 2, 3])
3
>>> water_height(5, [1, 0, 2, 1])
1

The function should have the following specification:

water_height.py

water_height(h0, rain_per_day)

Calculate the final water height after multiple days of rain.

Parameters:

h0	float	Initial height of the water in the reservoir.
rain_per_day	list of float	List of daily rainfall amounts.

Returns:

float

Final height of the water after accounting for daily rainfalls and evaporation.

Problem 6.16: Special Occurrence

Given a sequence of positive integers, we want to find what we call a special occurrence. A special occurrence is when the number 5 is followed by two numbers where exactly one is 7. Thus the occurrence …5, 3, 7… is a special occurrence, and so is the occurrence …5, 7, 8…, while …5, 7, 7… is not a special occurrence.

Write a function that takes as input a list of positive integers. The function should return the index of the number 5 in the first special occurrence. If no such occurrence exists, the function should return -1.

As an example, consider the sequence [2, 8, 11, 3, 12, 5, 7, 7, 11, 3, 12, 5, 2, 7, 5, 7, 2, 6]. The number 5 occurs three times in the sequence, at positions with index 5, 11, and 14. The first occurrence of the number 5 is not a special occurrence as it is followed by two 7. The second occurrence is a special occurrence as it is followed by 2 and 7. The third occurrence is a special occurrence, but it occurs later than the second occurrence. Therefore, the function should return 11, as shown below.

>>> special_occurrence([2, 8, 11, 3, 12, 5, 7, 7, 11, 3, 12, 5, 2, 7, 5, 7, 2, 6])
11

The filename and requirements are in the box below:

special_occurrence.py

special_occurrence(sequence)

Return the index of the first special occurrence.

Parameters:

sequence

list

A list of positive integers with 0 or more elements.

Returns:

int	The index of the first 5 followed by two numbers where exactly one is 7.

Use the following script to check your function test_special_occurrence.py. If your function fails the test in this script, it will also fail when you hand it in.

Problem 6.17: First Double Peak

Given a list of numbers, we want to locate the first peak. Usually, a peak is a number that is strictly larger than its first neighbors (the number just before and the number just after). However, in this task, we want to locate a double peak, which is a number that is strictly larger than both its first and its second neighbors (the two numbers before and the two numbers after).

Write a function that takes as input a list of floats. The function should return the index of the first double peak. If there is no double peak, the function should return -1.

As an example, consider the list [1.2, 2.4, 3.1, 2.9, 3.6, 2.3, 1.9, 2.4]. The numbers from the list are also in the figure below, where the x-axis represents the index of the numbers and the y-axis represents the values of the numbers.

Considering all numbers in order, the first two values should be ignored, as they have no two neighbors before. The value 3.1 a not strictly larger than its second neighbor with the value 3.6. The value 2.9 is not a peak either, as it is not strictly larger than 3.1. The value 3.6 (red) is a double peak as it is larger than both 3.1, 2.9, 2.3 and 1.9 (gray). The function should therefore return the index of the value 3.6. which is 4, as shown in the code cell below.

>>> first_double_peak([1.2, 2.4, 3.1, 2.9, 3.6, 2.3, 1.9, 2.4])
4

The filename and requirements are in the box below:

first_double_peak.py

first_double_peak(sequence)

Return first number strictly larger than its first and second neighbors.

Parameters:

sequence

list

A list of floats.

Returns:

int	The index of the first peak.

Use the following script to check your function test_first_double_peak.py. If your function fails the test in this script, it will also fail when you hand it in.