Week 5: In-Class

Coding Practice

Code 5.1: Fall Duration

The distance traveled by an object falling from rest is given by the formula

\[s = \frac{1}{2}g t^2\, , \]

where \(s\) is the distance traveled (in meters), \(t\) is the duration of the fall (in seconds), and \(g\) is the gravitational acceleration on Earth, equal to \(9.81\mathrm{m}/\mathrm{s}^2\).

Pen & Paper

For height a height of 100 meters, calculate the fall duration. Choose four additional heights of your own and calculate the fall duration for each.

Demo

Write a function fall_duration that takes as input the fall distance traveled (in meters) and returns the fall duration (in seconds).

Code 5.2: Customized Greeting

It is a custom to greet people differently depending on the time of day. We use a convention that morning starts at 4:30, and lasts until 12:00 when afternoon begins. At 17:30 evening starts, and night starts at 23:00. Morning, afternoon, evening, and night are marked with green, red, light blue and dark blue colors, respectively, in the figure below.

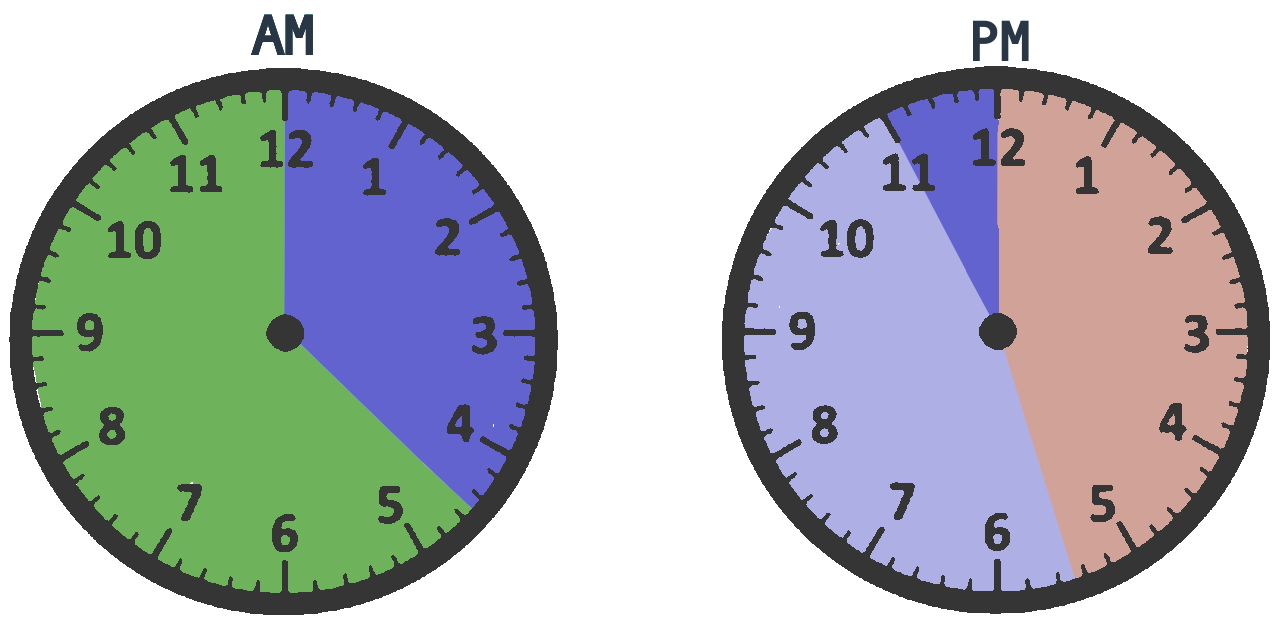
We want to determine a suitable greeting based on the time of day: Good morning!, Good afternoon!, Good evening!, or Good night!. Each time period includes its starting time but excludes its ending time. For example, 4:30 is morning, but 12:00 is afternoon.

Pen & Paper

According to the convention above, write down what the greeting should be for the following times of day: 7:00, 12:30, 18:15, 23:45, and 3:15. Also, determine the correct greeting for times just before and just after each boundary. Finally, notice that night includes times before midnight, and after midnight. Write down the time for both these periods.

Demo

Write a function customized_greeting that returns a polite greeting based on the time of day. The function should take two arguments: hours and minutes.

The argument hours is the hour of the day given in 24-hour format, so it is an integer between 0 and 23. The argument minutes is the minutes of the hour, given as an integer between 0 and 59. The function should return the correct greeting as a string, for example, "Good morning!".

Code 5.3: Function Testing (Buddy-Exercise)

Writing tests for functions often involves just as much work as writing the functions themselves and is just as important. One can write tests before writing the function. You can even write tests for functions which you do not know how to implement yet. For example, say you know that the function count_a should count the number of times the lowercase letter a appears in a string. You have not yet learned how to write such a function, but you can still write tests for it.

For this, you can make a dummy implementation of the function that always returns the same value, for example 0. Then, you can write and run tests. Since the dummy implementation does not do what it is supposed to, the tests will fail.

def count_a(s):
    return 0

test1 = count_a("banana") == 3
test2 = count_a("apple") == 1  # starting with 'a'
test3 = count_a("drape") == 1  # containing 'a' 
test4 = count_a("milla") == 1  # ending with 'a'
test5 = count_a("cherry") == 0  # no 'a's
test6 = count_a("") == 0  # empty string
test7 = count_a("Aardvark") == 2  # case sensitivity
test8 = count_a("aaaaaa") == 6  # all 'a's
all_tests_passed = (test1 and test2 and test3 and test4 and test5 and test6 
        and test7 and test8)

print("All tests passed:", all_tests_passed)
if not all_tests_passed:
    print("Individual test results:", test1, test2, test3, test4, test5, test6, 
            test7, test8)

All tests passed: False
Individual test results: False False False False True True False False

As you can see, a dummy solution may still return a correct value for some test cases, but it will fail for others. It is therefore important to write a variety of test cases that cover different scenarios, as we did in the example above. If you were given a function that passes all the tests, it would be an indication that the function is correct. You could then add additional tests to further verify the function.

For the next two exercises (Number Digits and Next Even), you practice writing functions and writing tests.

Student A

Write the function number_digits in the file number_digits.py. Then, write the test for next_even in the file next_even_test.py. You should not create a solution for the next_even function, but instead write a dummy solution that always returns 0.

Student B

Write the function next_even in the file next_even.py. Then, write the test for number_digits in the file number_digits_test.py. You should not create a solution for the number_digits function but may include a dummy solution that always returns ''.

Now send the files to each other, so that you both have all four files, and place these four files in the same folder. Together, test both functions using two different strategies:

• Test the number_digits function by copying the test code (without the dummy function) to the file where the function is written, and executing this file.

• Test the next_even function by importing the function into the test file and running the test file. That is, you should write

from next_even import next_even

in the first line of the test file. This will allow you to call the function next_even in the test file. Remember to delete the dummy function in the test file.

If your functions do not pass the tests, debug them together. Remember that the bugs can be in the function and in the test.

Code 5.4: Number Digits

Write a function number_digits that takes a positive integer as input and returns the number of digits in the number.

The test for this function should contain at least six different positive integers with varying numbers of digits.

Hint

You can convert the integer to a string and then use the len function.

Code 5.5: Next Even

You should write a function next_even that takes an integer n as input and returns the next even number. That is, if n is even, the function should return the even number that is 2 greater than n. If n is odd, the function should return the even number that is 1 greater than n. The function should work for both positive and negative integers.

The test for this function should contain numbers that are positive, negative, even, and odd. Also include test for the number 0.

Hint

You can test whether a number is even or odd using the modulus operator %. For example, n % 2 is 0 if n is even, and 1 if n is odd. Then, you can decide whether to add 1 or 2 to n to get the next even number.

Code 5.6: Cylinder Volume

The volume of a cylinder is given by the formula \(V = A h\), where \(A\) is the area of the base of the cylinder, and \(h\) is the height of the cylinder. The area of the base is given by the formula \(A = \pi r^2\), where \(r\) is the radius of the base.

Write first the functions disc_area that takes the radius of a disc as input and returns the area of the disc. Use math.pi as the value of \(\pi\), and remember to import the math module. Test your function.

Hint

You can use the following code to test your solution by comparing the expected output with the output of your function. This is only an indication (but not a guarantee!) that your solution is correct. For example, if you made a mistake and returned a string instead of a number, you would not notice this mistake by looking at the output.

print("Radius 1, expected disc area: 3.1415926535898, got:", disc_area(1))
print("Radius 2.8, expected disc area: 24.6300864041440, got:", disc_area(2.8))
print("Radius 14.5, expected disc area: 660.5198554173, got:", disc_area(14.5))

Hint

The following code provides better tests, as it compares the output of the function with the expected output. When comparing floating-point numbers, instead of using == it is better to check whether the two numbers are very close. This is because two correct solutions can be slightly different due to the way floating-point numbers are stored in the computer.

test1 = math.isclose(disc_area(1), 3.1415926535898)
test2 = math.isclose(disc_area(2.8), 24.6300864041440)
test3 = math.isclose(disc_area(14.5), 660.5198554173)

all_tests_passed = test1 and test2 and test3
print("All tests passed:", all_tests_passed)
if not all_tests_passed:
    print("Individual test results:", test1, test2, test3)

Now, in the same file, write the function cylinder_volume that takes the radius and height of a cylinder as input and returns the volume of the cylinder. Can you write cylinder_volume in a way such that it uses (calls) disc_area?

Here, disc_area is a helper function for cylinder_volume. A helper function may be placed in the same file as the main function, or in a separate file that is imported similar to how you imported tests earlier today.

Problem Solving

Problem 5.7: Parts to Ratio

When mixing liquids, the mixing instructions are often given in parts. For example, instructions to mix elderflower syrup with water might say 1 + 4, which means that you should mix one part elderflower syrup with four parts water. Given such instructions, we are interested in knowing the ratio of the one part in relation to the total liquid. Again looking at the example 1+4, the obtained mixture has \(1 + 4 = 5\) parts in total, and the elderflower syrup is one part of this. Therefore, the ratio of elderflower syrup to the total liquid is \(\frac{1}{5} = 0.2\).

Write a function parts_to_ratio that takes two arguments, part and part_other, and returns the ratio of part in relation to the total liquid.

Hint

You can use the following code to test your solution by comparing the expected output with the output of your function.

import math

test1 = math.isclose(parts_to_ratio(1, 2), 1/3)
test2 = math.isclose(parts_to_ratio(3, 2), 3/5)
test3 = math.isclose(parts_to_ratio(5, 4), 5/9)
test4 = math.isclose(parts_to_ratio(1, 1), 1/2)
test5 = math.isclose(parts_to_ratio(7, 3), 7/10)
test6 = math.isclose(parts_to_ratio(2, 3), 2/5)
test7 = math.isclose(parts_to_ratio(4, 4), 4/8)

all_tests_passed = (test1 and test2 and test3 and test4 and test5 and test6 
        and test7)
print("All tests passed:", all_tests_passed)

Problem 5.8: Dilute Solution

We want to dilute a solution by mixing it with a solvent. The mixing proportions are given in parts. The solution has a certain concentration, and after mixing it with the solvent, the concentration will be lowered. We want to compute the new concentration of the solution after it is mixed.

For example, consider having a solution that has a concentration of \(0.5\) g/L and mixing 2 parts of solution with 3 parts solvent. The resulting solution has \( 2 + 3 = 5 \) parts, of which 2 parts are the original solution. Therefore, the resulting concentration after dilution is \(\frac{2}{5}\cdot 0.5 = 0.2\) g/L.

Write a function dilute with arguments concentration, part_solution, and part_solvent that returns the concentration of the diluted solution.

Check

Check your solution by following the instructions below and comparing your result with ours.

• Make a solution with 50 g/L of NaCl in water.

• Dilute 2 parts of the solution with 3 parts of water.

• Dilute it again by mixing 1 part of the previous solution with 4 parts of water.

• Dilute it again by mixing 9 parts of the previous solution with 1 part of water.

• The final concentration of the solution should be 3.6 g/L.

Problem 5.9: Profit Margin

Profit margin measures the percentage of revenue that remains as profit after costs. The profit margin is calculated as

\[ \frac{r - c}{r} \]

where \(r\) is the revenue and \(c\) is the cost.

Create a function called profit_margin that receives two parameters, cost and revenue, and returns the profit margin as a percentage. The following companies would like to know how much profit margin they have made in the last year. Use the function to calculate the profit margin for each company. We use 10**9 for a billion.

Company	Cost ($)	Revenue ($)	Profit Margin (%)
Lemonade stand inc.	20	40	50
Floormart	30 billion	31 billion
Ztartup	200000	144000
Orange Inc.	60 billion	83 billion

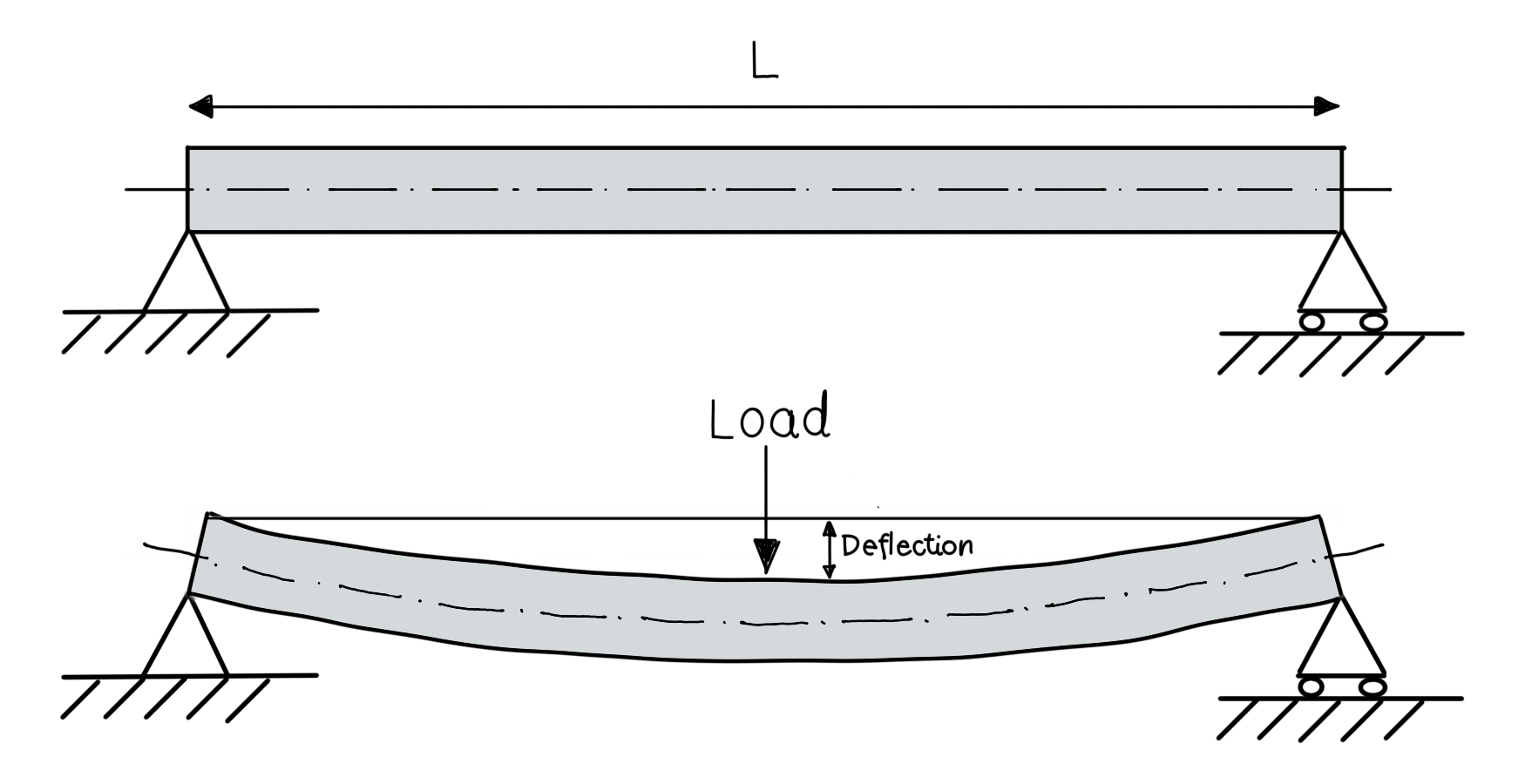
Problem 5.10: Beam Deflection

The deflection of a beam is given by

\[ D = \frac{M L^3}{3 \lambda I} \]

where \(D\) is the deflection, \(M\) is the load, \(L\) is the length of the beam, \(\lambda\) is the modulus of elasticity, and \(I\) is the moment of inertia. The illustration below shows an unloaded and a loaded beam.

Write a function that calculates the deflection of a beam. The function should have the following signature:

calculate_beam_deflection.py

calculate_beam_deflection(length, load, modulus_of_elasticity, moment_of_inertia)

Calculate the deflection of a beam under a load.

Parameters:

length	float	The length of the beam (m).
load	float	The load applied to the beam (N).
modulus_of_elasticity	float	The modulus of elasticity of the beam material (Pa).
moment_of_inertia	float	The moment of inertia of the beam’s cross-section (m${}^4$).

Returns:

float

The deflection of the beam (m).

How to test this function? Consider first setting all parameters to 1 and calculate the expected result by hand. See if your function returns the same result. Try some more interesting values and see if the function returns the expected result.

Problem 5.11: Wind Chill

Wind chill is the lowering of body temperature due to the flow of cool air. The perceived temperature is the wind chill temperature \(T_{WC}\). The cooling effect depends on air temperature \(T\) and wind speed \(v\) with the formula:

\[ T_{WC} = 13.12 + 0.6215 T - 11.37 v^{0.16} + 0.3965 T v^{0.16} \]

where \(T\) is the temperature in degrees Celsius and \(v\) is the wind speed in km/h.

Write a function that takes as input the actual temperature (in degrees Celsius) and the wind speed (in km/h). The function should return a string in the format X degrees with Y km/h wind feels like X degrees., where X is the actual temperature rounded to the nearest integer, Y is the wind speed rounded to the nearest integer, and Z is the perceived temperature rounded to the nearest integer.

Tip

Copy the string above and paste it into your code editor. This way you avoid typos and having to look up how to type the degree symbol.

To test your function, we have supplied test_wind_chill.py. You can run this file to see if your function is working as expected. The file runs the following four tests and checks if the output matches the expected outputs shown below.

>>> wind_chill(-3.6, 25)
'-4 degrees with 25 km/h wind feels like -11 degrees.'

wind_chill.py

wind_chill(temperature, windspeed)

Calculate the wind chill index based on the temperature and wind speed.

Parameters:

temperature	float	The actual temperature in degrees Celsius.
windspeed	float	The wind speed in km/h.

Returns:

str	A string describing the wind chill effect.

Problem 5.12: Bacterial Growth

We grow bacteria in a closed container that can sustain a certain number of bacteria. To investigate bacterial growth, we use the model

\[ \Delta N = r N \left(\frac{K - N}{K}\right) \]

where \(\Delta N\) is the change in the number of bacteria from one hour to another, \(r\) is the hourly growth rate, \(N\) is the number of bacteria, and \(K\) is the maximum number of bacteria that can be in the container. The expression in the parentheses is the fraction of the container that is empty. So if no space is empty and \(N = K\) the number of bacteria will not increase further.

Starting from an initial population, we want to know how many hours it will take for the bacteria to fill more than 90% of the container.

Consider \(N=100\), \(r=0.1\), and \(K=1000\). After one hour, the population will be 109, then approximately 118.7, 129.2, 140.4, and so on. The population will reach 90% of the maximum population after 44 hours.

Create a file called bacterial_growth.py. In this file create a function with the following specifications:

bacterial_growth.py

bacterial_growth(initial, growth_rate, max_bact)

Simulates bacterial growth over one week and returns the time taken to reach 90% of the maximum population.

Parameters:

initial	float	The initial number of bacteria.
growth_rate	float	The growth rate of the bacteria.
max_bact	float	The maximum population of the bacteria.

Returns:

int	The number of hours for the bacteria to reach 90% of the maximum population. Returns -1 if the population does not reach 90% within one week.

One expected output is shown below.

>>> bacterial_growth(100, 0.1, 1000)
44

You should also test your function with test_bacterial_growth.py.

Problem 5.13: Which Fibonacci?

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. The sequence starts as follows:

\[ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, \ldots \]

Create a function which_fibonacci that takes an integer as input, and returns which position this integer has in the list of fibonacci numbers. If the number is not in the list, the function should return -1.

To avoid ambiguities, you can assume the input is 2 or greater.

For example, the number 5 is the 6^th fibonacci number, so which_fibonacci(5) should return 6. Here are some additional examples:

>>> which_fibonacci(5)
6
>>> which_fibonacci(14)
-1
>>> which_fibonacci(14930352)
37

The function specifications are:

which_fibonacci.py

which_fibonacci(n)

Determines which Fibonacci number the input is.

Parameters:

n

positive int

The number we wish to test.

Returns:

int	The position in the list of Fibonacci numbers. If it is not in the list, return -1.

Exit Tickets as Assignments. As before, the exit ticket exercises (marked with ) are adapted from past exam questions. You should attempt them without help to check your understanding of the material.

Now that we have learned functions, we can formulate the tasks in the same way they will appear on exams. Starting this week, you may submit your exit ticket solutions under the Assignments tab. We regularly test all submitted solutions and provide feedback. If the feedback reveals mistakes, you are welcome to correct them, re-submit your work, and have your submission graded again. There are no fixed deadlines for these submissions, but don’t postpone them just because there is no deadline.

Problem 5.14: Normal Range

The body mass index (BMI) is defined as

\[ BMI = \frac{w}{h^2} \]

where \(w\) is body weight (mass) in kilograms, and \(h\) is the height in metres. A person is categorized as being of normal weight if their BMI falls in the range from \(18.5\frac{kg}{m^{2}}\) to \(25\frac{kg}{m^{2}}\), both endpoints included.

Write a function that takes a height in meters as input. The function should return a string Normal weight range: X to Y kg with the normal weight range, where X and Y are the smallest and the largest weight in whole kilograms, which when converted to BMI fall into normal range, respectively.

Consider the height \(1.73\). The weight limits for the normal range can be calculated as \(w_{lower} = 18.5 \cdot h^2\) and \(w_{upper} = 25 \cdot h^2\). The weight should be expressed in whole kilograms, so both limits should be rounded. To ensure that weight falls into the normal range, the lower limit should be rounded up and the upper limit should be rounded down.

You can see the desired behavior below.

>>> normal_range(1.73)
'Normal weight range: 56 to 74 kg'

The filename and requirements are:

normal_range.py

normal_range(height)

Calculates the normal weight range based on height.

Parameters:

height

float

The height of the person in meters.

Returns:

str	A string indicating the normal weight range in kilograms.

Use the following script to check your function test_normal_range.py. If your function fails the test in this script, it will also fail when you hand it in.

Problem 5.15: Lucas Number

The Lucas sequence is an integer sequence similar to the Fibonacci series. Every Lucas number is a sum of the previous two Lucas numbers, given that the first two Lucas numbers are 2 and 1. That is, Lucas numbers are defined by

\[\begin{split} L_i = \begin{cases} 2 & \text{if } i = 0, \\ 1 & \text{if } i = 1, \\ L_{i-1} + L_{i-2} & \text{otherwise.} \end{cases} \end{split}\]

The start of the Lucas sequence is 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, …

Write a function that, given an index \(i\), returns the Lucas number with that index, that is \(L_i\).

For example, if the input is \(i = 3\) the function should return \(L_3\). We can start by using \(L_1\) and \(L_0\) to form \(L_2 = L_1 + L_0 = 3\). Similarly we continue with \(L_2\) and \(L_1\) to compute \(L_3 = L_2 + L_1 = 3 + 1 = 4\). Therefore the function should return \(4\).

The desired behavior is shown below.

>>> lucas_number(3)
4

The filename and requirements are:

lucas_number.py

lucas_number(i)

Finds the Lucas number at the given index.

Parameters:

i

int

Index of the Lucas number to find.

Returns:

int	The Lucas number at the given index.

Use the following script to check your function test_lucas_number.py. If your function fails the test in this script, it will also fail when you hand it in.