Closure

Closure#

Syllabus week 5: Functions#

  • Functions, keyword def

  • Function names and naming convention

  • Function parameters (names given by the function definition)

  • Function arguments (values passed to the function when called)

  • Function body and indentation

  • Calling functions

  • Variable scope

  • Returning values, keyword return

  • Fruitful and void function, side effects, None type

  • Function examples: build-in functions, functions included in the standard Python library, functions from common third-party libraries, user-defined functions.

  • Tracebacks in error messages

  • Good practice when writing functions (start by scripting, incremental development, scaffolding)

  • Testing functions

  • Writing tests for functions

  • Documenting functions

Advanced#

Note about the material in Advanced section. The advanced material contains more some additional topics related to the weeks’s content. You are not required to read this material, and none of the exercises or exam questions will rely on this material.

Some additional concepts to familiarize yourself with are:

Advanced 5.1: Fibonacci Sequence with Recursion#

Hint

You will probably need 3 variables to keep track of the numbers. You can start with f=0 f_next=1 and f_next_next=1. Then you can update the variables in a loop.

Fibonacci with recursion

Recursive functions are functions which call themselves. An example of a recursive implementation of the factorial is included below. How many times is the function called if you want to calculate the factorial of 5? Consider adding a print statement to the function to see how many times it is called.

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

Now, write a recursive function fibonacci_recursive that takes \(n\) as an input and returns the \(n\)th number in the Fibonacci sequence. The function should use recursion to calculate the numbers in the sequence (not a loop).

Advanced 5.2: More About Divisions#

The following exercises use the is_divisible function from the In-Class exercises.

Printing all factors

A factor is a number that divides another number without leaving a remainder. Given a number, we want to know all the numbers that are factors of that number. For example, take the number 12. Looking at all numbers from 1 to 12, we see that 12 is divisible by 1, 2, 3, 4, 6, and 12.

Use is_divisible function to write a function all_factors that takes num as input and prints all the factors of num. For example all_factors(12) should print

1
2
3
4
6
12

Number of times divisible

We want to extend the is_divisible function to return the number of times a number is divisible by another number. For example take the number 12 and divisor 2. If we divide 12 by 2, we get 6, and if we divide 6 by 2, we get 3, which is not divisible by 2. Therefore, 12 is divisible by 2 two times.

Use is_divisible function to write a function num_times_divisible which should alto take two arguments num and divisor. If num is not divisible by divisor, the num_times_divisible function should return 0. If num is divisible by divisor, the function should return the number of times num is divisible by divisor. For example, num_times_divisible(12, 2) should return 2.

Advanced 5.3: Prime Numbers and Factorization#

Also these exercises continue the theme of divisibility.

Is prime

Write a function, is_prime which returns True when a num is prime and False if not. You may have code from a previous week that does this, consider reusing this in the function. If not, a prime number is defined by having only two factors, 1 and itself. So for example, is_prime(7) should return True since 7 is not divisible by 2,3,4,5 and 6. is_prime(6) should return False since 6 is divisible by 2 and 3. A small note: 1 is not a prime number since it only has one factor.

Print prime factors

Any number can be written as a product of prime numbers. For example, \(12\) can be written as \(2 \cdot 2 \cdot 3\), \(13\) can be written as just \(13\) (because it is prime), \(14\) can be written as \(2 \cdot 7\), and so on. Write a function that takes a number as an argument and prints all the prime factors of that number. Feel free to use previous functions you have written. If everything has went well, print_prime_factors(12) should print

2
2
3

and print_prime_factors(13) should print

13

and print_prime_factors(72) should print

2
2
2
3
3

Advanced 5.4: Default Arguments, Positional and Keyword Arguments#

Default arguments is a way to set a value for an argument if the function is called without that argument. For example, consider the following function which approximates the square root of a number using Newton’s method

def approximate_square_root(x, epsilon=1e-6, max_iter=100, guess=1.0):
    print("Arguments:\nx:", x, "epsilon:", epsilon, "max_iter:", max_iter, "guess:", guess)
    converged = False
    for i in range(max_iter):
        if abs(guess**2 - x) < epsilon:
            converged = True
            break
        guess = (guess + x / guess) / 2
    if not converged:
        print("Did not converge in", max_iter, "iterations. epsilon:", epsilon)
    return guess
print("Actual sqrt(2) = ", 2**0.5)
print("result:",approximate_square_root(2, 1e-6, 100, 1.0))
print("result:",approximate_square_root(2))
print("result:",approximate_square_root(2, 1e-15))
print("result:",approximate_square_root(2, 1e-15, 2))

In the function above, epsilon has a default value of 1e-6. For all the arguments we have:

  • x has no default value, so it must be provided when calling the function.

  • epsilon has default value 1e-6.

  • max_iter has default value 100.

  • guess has default value 1.0.

A keyword argument is when you pass an argument with a keyword and a value, like epsilon=1e-6. For example, in the code above, try calling the following

print(approximate_square_root(2, epsilon=1e-10))
print(approximate_square_root(2, max_iter=1000))
print(approximate_square_root(2, guess=100, max_iter=2))
print(approximate_square_root(max_iter=1, x=2))

The keyword notation allows you to pass the arguments in any order, as long as you specify the keyword. If there is a default value, you can also omit the argument (e.g. we don’t need to pass epsilon if we want to use the default value).

A positional argument is when you pass an argument without a keyword, like 2. For example, approximate_square_root(2, 1e-10, 5, 1) only uses positional arguments. Try calling the following (it should give an error!):

print(approximate_square_root(2, guess=1.0, 1e-10))

Python does not allow positional arguments after keyword arguments. This is because it can be ambiguous which argument is which. Python cannot guess if you want 1e-10 to be epsilon or max_iter. You also get an error if you try to pass the same argument twice:

print(approximate_square_root(x=2, x=3))

Advanced 5.5: Global Variables#

In the preparation, you have seen that you can use global variables. In this course, you should avoid using global variables. Try this code to see how it can be rather confusing to figure out what can be changed and what cannot. First run the code as-is. Then, try uncommenting first the one, and then the second commented line. Lastly, try uncommenting both lines.

some_number = 10

def some_function():
    # some_number = 3
    print(some_number)
    a = 5 + some_number
    # some_number = 14
    return a

k = some_function()
print(k)
print(some_number)

10
15
10

Advanced 5.6: Order of Defining Functions#

When you define a function, you can’t call it before it’s defined. This is because Python reads the code from top to bottom. If you try to call a function before it’s defined, you’ll get an error. Here is an example. Fix the code so that it runs without errors.

display_sad_message()
def display_sad_message():
    print("aw man D:")

For functions that call other functions, you can actually define the functions in any order as long as they are all defined before you call any of them. Here is an example.

def calc_kinetic_energy(mass,distance, time):
    velocity = calc_velocity(distance, time)
    kinetic_energy = 0.5 * mass * velocity ** 2
    return kinetic_energy
# calc_kinetic_energy(1,2,3) # This should raise a an error
def calc_velocity(distance, time):
    return distance/time
print("The kinetic energy is:", calc_kinetic_energy(1, 2, 3))

Try to run the code (it should work unchanged). Try to uncomment the line with # and see what error you get.

Advanced 5.7: Naming Functions#

An important aspect of writing functions is to name them appropriately. For example, consider a function which calculates the volume of a cone. A good name for this function would be cone_volume. This name is descriptive and tells you what the function does.

def cone_volume(radius, height):
    pi = 3.141592653589793
    return pi * radius**2 * height / 3

Note that the function name is in lowercase and uses underscores to separate words. This is the convention in Python, however it is not a strict rule and if you want to be different you could name your function ConeVolume, coneVolume or cONeVoLUme but it would likely confuse other Python programmers. A bad name for this function would be cone, vol or func since these functions don’t describe what it does appropriately. Sometimes it is useful to add a prefix to the function name to indicate what action the function does. The function above could be named calc_cone_volume. Other useful prefixes could be:

  1. print_XXX or display_XXX: If your function prints something.

  2. calc_XXX, estimate_XXX, or get_XXX: If your function calculates something and/or returns it.

  3. update_XXX or change_XXX: If your function updates or modifies something.

  4. check_XXX, is_XXX or has_XXX: If your function checks something (i.e. returns True if what it checks is true and False otherwise).

Match the following functions with an appropriate prefix:

def volume(vol):
    print("My volume is", vol)

def right_triangle(a,b,c):
    return a**2 + b**2 == c**2

def triangle_type(a,b,c):
    if a == b == c:
        return "equilateral"
    elif a == b or b == c or a == c:
        return "isosceles"
    else:
        return "scalene"

Solution

  1. volume -> print_volume or display_volume

  2. right_triangle -> check_right_triangle or is_right_triangle

  3. triangle_type -> get_triangle_type

Advanced 5.8: Central Number#

Given three numbers, we want to know which one is the central number. When the three numbers are all different, the central number is the one that is neither the largest nor the smallest. If two or more of the numbers are the same, the central number is that number.

Write a function central_number(a, b, c) that takes three numbers as arguments and returns the number which is central.

Advanced 5.9: Greatest Common Divisor#

The greatest common divisor (GCD) of two numbers (non-negative integers) is the largest number that divides both numbers. For example, the GCD of 12 and 18 is 6. Write a function greatest_common_divisor that takes two numbers as arguments and returns GCD. This is useful if you want to simplify a fraction. For example, the GCD of 12 and 18 is 6 and therefore

\[\frac{12}{18} = \frac{12/6}{18/6} = \frac{2}{3}.\]

If your implementation is correct, then you should expect the results shown in the table below.

num1

num2

GCD

12

18

6

10

15

5

1024

192

64

100

1000

100

1000

100

100

23

23

23

Consider the following code. It specifically tests the first example from the table above.

expected = 6
output = greatest_common_divisor(12, 18)
if output != expected:
    print("FAILED the following test:")
print("greatest_common_divisor(12, 18) returned", output, "should be", expected)

A complete test of all the expected outputs from the table is available in test_greatest_common_divisor.py. Download this file, then run the test function to test your code. Make sure it imports the function from your file greatest_common_divisor.py. It will only work if

  • your file is called greatest_common_divisor.py,

  • your function inside the file is called greatest_common_divisor,

  • the files greatest_common_divisor.py and test_greatest_common_divisor.py are in the same directory.

Advanced 5.10: Falling Ball Simulation#

In this exercise, you will simulate a falling ball by making a loop over time. You will calculate how the acceleration, velocity and position (height) change at each time step. We want to know how long it takes for the ball to hit the ground. The simulation will stop when the ball hits the ground or when the maximum number of time steps is reached.

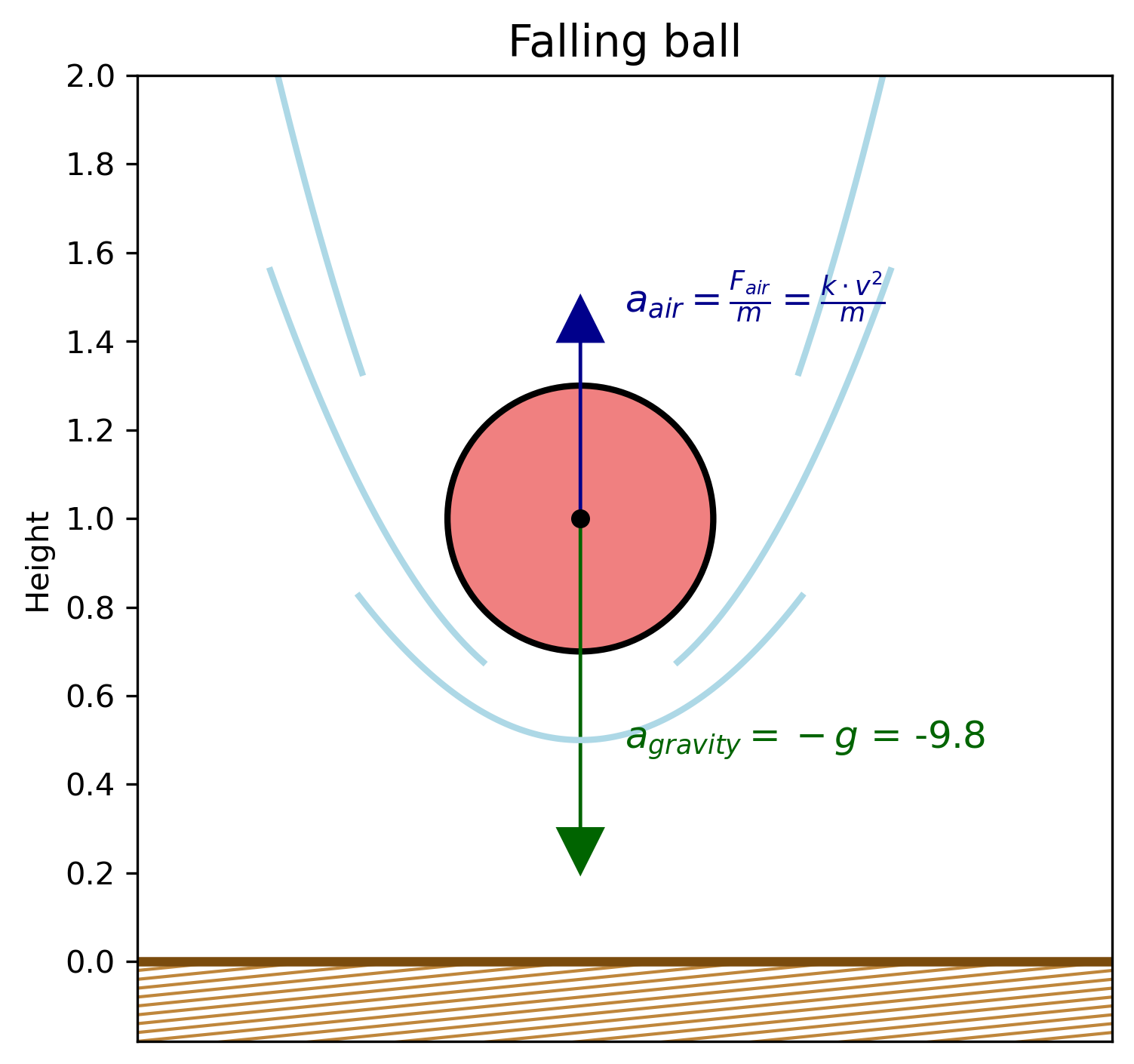
image

The simulation will include the following parameters (they are inputs to the simulation):

  • Initial height of the ball in meters (variable name: h0).

  • Time step size in seconds (variable name: dt).

The simulation will include the following variables which will change at each time step in the loop:

  • Height of the ball in meters (variable name: h).

  • Velocity of the ball in \(m/s\) (variable name: v).

  • Acceleration of the ball in \(m/s^2\) (variable name: a).

For now, we will ignore air resistance. The only force acting on the ball is the gravitational force. The acceleration due to gravity is a constant known as \(g=9.8 m/s^2\) which means the acceleration is

\[a=-g=-9.8 m/s^2.\]

The sign of the acceleration is negative since gravity points downward, and similarly a downward velocity is negative. To update the velocity for a single time step, you can use the formula

\[ v_{new} = v_{old} + \Delta v = v_{old} + a \cdot \Delta t.\]

and similarly, to calculate the new position (height) for a single time step, you can use the formula

\[ h_{new} = h_{old} + \Delta h = h_{old} + v \cdot \Delta t,\]

Simulation without air resistance

You can use this script to get started, where we simply drop the ball from 1 meter.

#Parameters:
h0 = 1.0 # initial height in meters
dt = 0.01 # time step size in seconds

#Initial values:
v = 0
h = h0

#Constants:
g = 9.8
max_time_steps = int(10/dt) # this corresponds to 10 seconds

for time_step in range(1,max_time_steps+1):
    t = time_step * dt
    #Your code here

Afterwards, add a loop and do the following computations at each time step:

  1. Get the acceleration (very simple in this case).

  2. Update the velocity.

  3. Update the position.

  4. Check if the ball has hit the ground (height is less than 0). If so, print the time it took for the ball to hit the ground and break the loop.

If your implementation is correct, then the ball should hit the ground after around \(\sqrt{2 h_0/g}=0.451754\) seconds, which is the theoretical time it takes for an object to fall from a height \(h_0\) without air resistance. The smaller the time step size, the more accurate the result should be.

Hint

Remember that when updating a variable in code, we don’t actually need two different variables for the old and new values. We can simply update the variable in place. For example, to update the velocity, you can write v = v + a*dt.

Hint

In case something isn’t working, maybe add a print statement similar to print("t:",t,"h:",round(h,2),"v:",round(v,2) every e.g. 10th time step to see what is happening.

Collect your script into functions

Now, you should have a script that simulates the falling ball. The next step is to collect the code into functions since this will make parameters much easier to change and the code more readable. Create the following functions:

  1. update_velocity: This function should take the velocity (v), acceleration (a) and time step size (dt) as input and return the updated velocity.

  2. update_position: This function should take the position (h), velocity (v) and time step size (dt) as input and return the updated position.

Define the functions, then replace the corresponding code in the simulation with function calls. The simulation should give the same result as before.

Now, wrap all the code in a function called falling_ball_simulation which takes the initial height h0 and the time step size dt as input.

>>> falling_ball_simulation(1, 0.01)
The ball has hit the ground after 0.45 seconds.

>>> falling_ball_simulation(100, 0.01)
The ball has hit the ground after 4.5200000000000005 seconds.

Simulation with air resistance

The air resistance is given by

\[F_{\text{air}} = 0.5 \cdot C_d \cdot A \cdot \rho \cdot v^2=k \cdot v^2.\]

For simplicity, we assume all the constants (everything except \(v\)) are lumped together into a constant \(k\) with the value \(0.0087\). The acceleration is now

\[a = a_{\text{air}} + a_{\text{gravity}} = \frac{k \cdot v^2}{m} - g.\]

We add 2 new parameters to the simulation:

  • The mass of the ball in kg (variable name: m).

  • A boolean with_air_resistance which is True if air resistance should be included and False if not (same as before).

Add air resistance to the simulation by writing the function get_acceleration. Update the falling_ball_simulation function to also include air resistance, and also take the additional inputs. The ball should take longer to hit the ground if air resistance is included.

get_acceleration(m, g, v, with_air_resistance)

Calculate the acceleration of an object.

Parameters:

  • m

positive float

Mass of the object (kg).

  • g

float

Acceleration due to gravity (m/s2).

  • v

float

Velocity of the object (m/s).

  • with_air_resistance

bool

If True, consider air resistance in the calculation.

Returns:

  • float

The acceleration of the object (m/s2).

Use the following parameters with your simulation, and find the time it takes for the ball to hit the ground in each case:

initial height

delta time

w/ air resistance

mass

1 m

0.001 s

no

0.3 kg

1 m

0.001 s

yes

0.3 kg

100 m

0.001 s

no

0.3 kg

100 m

0.001 s

yes

0.3 kg

100 m

0.001 s

yes

5 kg
Contents