Week 3: Conditionals, recursion, and frutiful functions

Important

You must start by downloading the script

download_week03.py

Right-click and select “Save link as…”. You may need to confirm the download in your browser.

Run this script in VSCode to download the code snippets and tests you need for week 3. The script does not need to be located a specific place on your computer.

If you get an error from the script, please follow the instructions in the error message. If you give up, proceed to the exercises (which you can still do), and ask a TA once they arrive.

The script should end with Successfully completed!, which means that you now have the tests for this week.

Videos (Watch this before the other videos)

Hello everyone! My name is Tue Herlau, and I asked Vedrana if I could upload a few videos for this exercise as an experiment. What I am going to cover is:

• What the videos are about and how to use them (please watch this first)

• A bit about common VS Code problems involving multiple interpreters (i.e., nearly all installation problems – I know this video will not fix everyones problem, but hopefully it can make it a little more clear; use Piazza and Discord!)

• How to start and use the interpreter

• How to work with scripts

• How to solve the exercises (but please see the first video!)

• How to use the test system (important)

• How to get started on the project and use the tests

Please note the videos are not a stand-in for the lectures or Think Python, which you should prioritize over my blabber :-).

Video 3a: Watch this first

Video 3b: Using VS Code and install problems

Exercise 3.1: Relational operators

Video 3.1: Exercise walkthrough

Subexercise a

Does each of the following bits of code print out True or False? Evaluate the expression on paper or in your mind first and verify your answers by pasting the code into the terminal.

• math.pi < 3

• with x = 10,

  • x < 5

• with x = 6,

  • math.pi > 3 and x > 5

  • math.pi > 3 or x < 5

• with x = 5,

  • math.pi > 3 and x == 5

Subexercise b

Define a variable y that is True when x is greater than 7.

Tip

Consider this code:

x = 45   # an example value
y = True # 'True' when x > 7

Replace y = True with an expression so that y is True with the given value of x > 7.

Subexercise c

Define a variable z that is True when x is smaller than \(\pi\).

Solutions

• a: False, False, True, True, True

• b: y = x > 7

• c: z = x < math.pi

Exercise 3.2: Logical operators

Video 3.2: Exercise walkthrough

Write some code that evaluates the follwoing statements to True or False. Evaluate the expression on paper first and verify your answers with your code.

Tip

• greater than or equal can be expressed as >=

• Not equal can be expressed as !=

• Equal can be expressed as ==

• either a or b can be expressed using a or b

• a and b can be expressed using a and b

• The cosine of \(x\) can be evaluated using math.cos(x)

• divisble by a number can be checked using the modulo operator %

Subexercise a

\(9\) is greater than or equal to \(3 \cdot 3\)

Subexercise b

\(91\) is not equal to \(11 \cdot 9\)

Subexercise c

Either \(2\) is greater than \(3\) or \(3 \cdot 3\) is not equal to \(9\)

Subexercise d

The cosine of \(3\pi\) is a negative number

Subexercise e

9 is greater than or equal to \(5\) and divisible by \(3\)

Subexercise f

The cosine of \(3\pi\) is a positive number or is equal to \(0\)

Subexercise g

Assign the value True or False to the variable y depending on x being greater than \(10\) and an even number. Try different values of x to verify your answer.

Tip

• even number can be checked using the modulo operator %2

• negative number translates to being less than \(0\)

• True and True evaluates to True

• True and False evaluates to False

• True or False evaluates to True

• False or False evaluates to False

Solutions

• a: 9>=3*3

• b: 91!=11*9

• c: (2>3 or 3*3!=9)

• d: math.cos(3*math.pi)<0

• e: 9>=5 and 9%3==0

• f: math.cos(3*math.pi)>0 or math.cos(3*math.pi)==0

• g: y = (x>10 and x%2==0)

Exercise 3.3: Function with return value

Video 3.3: Exercise walkthrough

Up to this point, you have been crafting Python functions that execute a series of computational steps and then print a message containing the result. However, in this exercise, we will construct a function that returns the result instead.

>>> def is_equal(a, b):
...     if a == b:
...         return "yes"
...     else:
...         return "no"
... 
>>> a = 2 + 4
>>> b = 3 + 5
>>> c = 2 * 4

Test the function is_equal() with different combinations of a, b and c and store the result in a variable result. Print the result outside of the function, e.g. print("Is a equal to b?", result). Notice how, instead of printing a message directly, the function is_equal() returns a value that is stored in the variable result, which can then printed outside of the function.

Optional Write your own function that checks if a is greater than b and returns the result.

Exercise 3.4: Classify body temperature using the if statement

Video 3.4: Exercise walkthrough

In this exercise, you will implement a function body_temperature that returns the body’s state based on the body’s temperature. The function should return a str depending on the temperature:

Open and closed intervals

An interval such as \([a, b]\) means all values \(a \leq x \leq b\) whereas for instance \(]a, b]\) means \(a < x \leq b\).

• If temperature is below \(35\), it should return "Hypothermia"

• If temperature is in the interval \([35, 37]\), it should return "Normal"

• If temperature is in the interval \(]37, 38]\), it should return "Slight fever"

• If temperature is in the interval \(]38, 39]\), it should return "Fever"

• If temperature is higher than \(39\), it should return "Hyperthermia"

Does your function return the right answer to the following examples?

>>> body_temperature(34.5)
'Hypothermia'
>>> body_temperature(35)
'Normal'
>>> body_temperature(38)
'Slight fever'
>>> body_temperature(39)
'Fever'
>>> body_temperature(39.5)
'Hyperthermia'

Tip

• Begin by implementing the if-statement for the lowest temperature range. Remember the return-keyword!

• For temperature ranges \([a, b]\), you can check these as if \(x\) is greater than \(a\) and \(x\) is less than \(b\)

• Consider using elif and else (not strictly necessary, but it will make your code more readable and robust)

To test your solution, add it to the file cp/ex03/body_temperature.py.

cp.ex03.body_temperature.body_temperature(temperature)

Calculate the body’s response based on the given temperature.

Parameters

temperature – The temperature in degrees Celsius.

Returns

The body’s response as a string.

Exercise 3.5: Comparing numbers

Video 3.5: Exercise walkthrough

In this exercise, you will implement a function compare_numbers that returns which of two numbers is greater. Think of appropriate arguments. The function should return a str as follows:

• if the first number is greater than the second number, the program should return "the first number is greater".

• if the second number is greater the program should display "the second number is greater".

• if both numbers are equal, the program should display "the numbers are equal".

Does you function work as intended? Test the following examples:

>>> compare_numbers(29,16)
'the first number is greater'
>>> compare_numbers(10,20)
'the second number is greater'
>>> compare_numbers(13,13)
'the numbers are equal'

Add your solution to the file cp/ex03/compare_numbers.py to run the tests.

cp.ex03.compare_numbers.compare_numbers(first_number, second_number)

Return a string based on which number has the greatest numerical value.

Parameters

• first_number (int) – first number.

• second_number (int) – second number.

Return type

str

Returns

string stating which number is the greatest.

Exercise 3.6: Blood alcohol concentration calculator

Video 3.6: Exercise walkthrough

Blood Alcohol Concentration (BAC) is a numerical measure of the amount of alcohol present in a person’s bloodstream. The calculation of BAC is influenced by several factors, including the person’s weight, gender, the amount of alcohol consumed, and the time elapsed since drinking, according to the equation:

\[BAC = \frac{A}{(r \cdot W)} \cdot 100 - \beta \cdot T\]

where

• \(A\) is the mass of alcohol consumed in kg.

• \(r\) is the distribution ratio. It is \(0.68\) for males and \(0.55\) for females.

• \(W\) is the body weight in kg.

• \(\beta\) is the rate at which alcohol is metabolized. It is \(0.015\) for males and \(0.017\) for females.

• \(T\) is the time elapsed since consumption in hours.

Note

There are several formulas used to estimate BAC, we are using one commonly used formula, the Widmark formula, which was developed by Swedish professor Erik Widmark in the 1920s.

Implement a function bac_calculator which takes the total amount of alcohol consumed alcohol_consumed, the person’s body weight weight, the person’s gender gender, and the time elapsed (in hours) since consumption time and returns the calculated blood alcohol concentration BAC.

Example: Suppose a 80 kg male consumes 28 grams of alcohol in total, and the time elapsed since alcohol consumption is 2 hours. As we are calculating the BAC for a male, we assume a distribution ratio of 0.68 and a \(\beta\) of 0.015, hence the BAC will be

\[BAC = \frac{0.028}{(0.68 \cdot 80)} \cdot 100 - 0.015 \cdot 2 \approx 0.0214 \%\]

or the same example in code (test if your function returns the same values):

>>> alcohol_consumed = 0.028  # Total alcohol consumed: 28 grams
>>> weight = 80.0             # Body weight: 80 kilograms
>>> time = 2                  # Time elapsed since alcohol consumption: 2 hours
>>> bac_calculator(alcohol_consumed, weight, "male", time) # BAC for a man
0.02147058823529411
>>> bac_calculator(alcohol_consumed, weight, "female", time) # Same for a woman
0.02963636363636364

Tip

• Note we specify the gender as the third argument as a str, which can be either "male" or "female"

• Use conditional statements (if-else) to determine the appropriate distribution ratio and elimination rate based on the gender. Use the provided values of 0.68 and 0.015 for male, and 0.55 and 0.017 for female.

Add your solution to the file cp/ex03/bac_calculator.py to run the tests.

cp.ex03.bac_calculator.bac_calculator(alcohol_consumed, weight, gender, time)

Calculate the blood alcohol concentration based on the alcohol consumed, body weight, and time since consumption.

Parameters

• alcohol_consumed (float) – The total amount of alcohol consumed in grams (float)

• weight (float) – The person’s body weight in kilograms (float)

• gender (str) – The person’s gender, which must be a string of either “male” or “female” (str)

• time (float) – The time elapsed since alcohol consumption in hours (float)

Return type

float

Returns

The calculated blood alcohol concentration (BAC) as a float value.

Exercise 3.7: Solar panel installation

Video 3.7: Exercise walkthrough

In this assignment, you will implement a function solar_panel that decides the ponderous question if we should put solar panels on something based on the following decision diagram developed by experts:

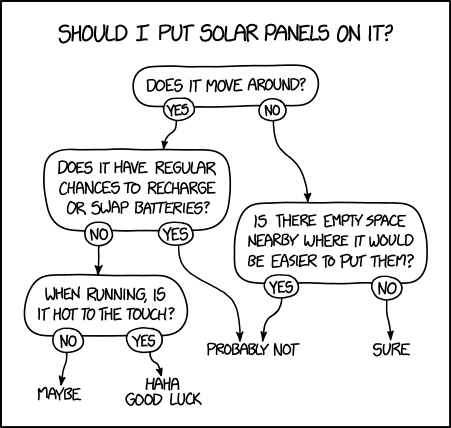
Decision tree for whether you should install solar panel on an object (source & copyright).

The function should take the following arguments and print out the appropriate answer according to the diagram:

• move: Does it move around?

• swap: Does it have regular chances to recharge or swap batteries?

• hot: When running is it hot to the touch?

• empty: Is there empty space nearby where it would be easier to put them?

These will have the value of either True or False.

Note

Note the last example below, where it should print out "haha, good luck", now works regardless of whether you use one or two lines (this is a change compared to the version shown in the video).

Try out the following examples:

>>> print("Should I install solar panel on the chimney?")
Should I install solar panel on the chimney?
>>> solar_panel(False, True, True, True)
'probably not'
>>> print("Should I install solar panel on the roof?")
Should I install solar panel on the roof?
>>> solar_panel(False, True, True, False)
'sure'
>>> print("Should I install solar panel on the windmill?")
Should I install solar panel on the windmill?
>>> solar_panel(True, False, False, False)
'maybe'
>>> print("Should I install solar panel on a fighter jet?")
Should I install solar panel on a fighter jet?
>>> solar_panel(True, False, True, False)
'haha, good luck'

This is a slight change compared to the video solution. Add your function to the file cp/ex03/solar_panel.py to test your solution.

cp.ex03.solar_panel.solar_panel(move, swap, hot, empty)

Print out whether it is a good idea to install solar panels on an object with the given properties.

Parameters

• move (bool) – does the object move around?

• swap (bool) – does the object allow swapping or recharging battery?

• hot (bool) – is the object hot to the touch when it is running?

• empty (bool) – are there other empty places near the object?

Return type

str

Returns

Whether you should put solar panels on the object as a string.

Exercise 3.8: Risk of heart attack

Video 3.8: Exercise walkthrough

Now, you will implement a function that determines the risk of a person having a heart attack based on the following decision tree:

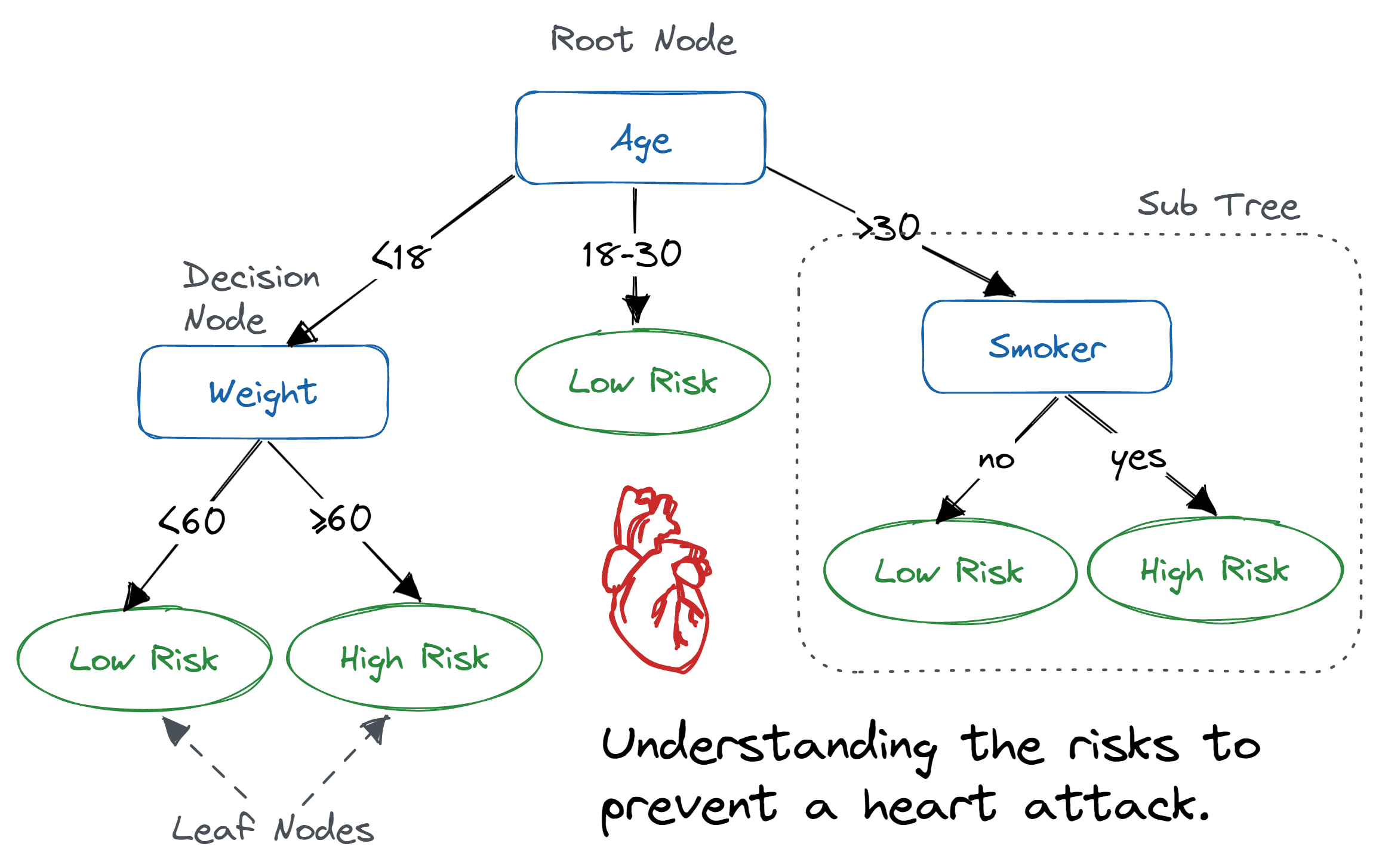
Decision tree for the risk of a person having heart attack (source).

Think about suitable arguments for the function and return low or high depending on the risk. Does your function return the same values as in the examples below?

>>> print("Risk for a 30-year-old, 45kg, non-smoking person?", heart_attack(30, 45, False))
Risk for a 30-year-old, 45kg, non-smoking person? low
>>> print("Risk for a 60-year-old, 70kg, smoking person?", heart_attack(60, 70, True))
Risk for a 60-year-old, 70kg, smoking person? high
>>> print("Risk for a 17-year-old, 40kg, smoking person?", heart_attack(17, 40, True))
Risk for a 17-year-old, 40kg, smoking person? low

Add your function to the file cp/ex03/heart_attack.py to test your solution.

cp.ex03.heart_attack.heart_attack(age, weight, smoker)

Return a string indicating the risk of a person for having heart attack.

Parameters

• age (int) – The age of the person.

• weight (int) – The weight of the person in kilograms.

• smoker (bool) – Does the person smoke cigarettes?

Return type

str

Returns

A string, either “low” or “high”, indicating the risk for having heart attack.

Exercise 3.9: Exponential function

Video 3.9: Exercise walkthrough

In this exercise, you will implement a function that computes the exponential of a number using recursion.

Given a base number \(x\) and the exponent \(n\), the exponential function computes the value \(x^n\), which can be obtained by multiplying \(x\) by itself for \(n\) times. Observe that the exponential problem has a recursive structure if \(n\) is a positive integer:

\[x^n = x \cdot x^{n-1}\]

This means we can also compute the exponential in a recursive manner:

\[\begin{split}f(x, n) = \begin{cases} 1 & \text{if } n = 0 \\\\ \frac{1}{ f(x, -n) } & \text{if } n < 0 \\\\ x \cdot f(x, n-1) & \text{otherwise} \end{cases}\end{split}\]

where we handle negative \(n\) by using the identity \(x^n=\frac{1}{x^{-n}}\).

Note

Obviously, the better way to compute the exponential function is as x**n. However, try to solve this exercise using recursion, i.e. without the ** operator or loops (a topic we will consider next week).

Do you get the right results? Try a few examples.

>>> print("3 to the power of 4 =", exponential(3, 4))
3 to the power of 4 = 81.0
>>> print("2 to the power of 5 =", exponential(2, 5))
2 to the power of 5 = 32.0
>>> print("4 to the power of -2 =", exponential(4, -2))
4 to the power of -2 = 0.0625

Add your function to the file cp/ex03/exponential.py to test your solution.

cp.ex03.exponential.exponential(x, n)

Compute the exponential \(x^n\) using recursion.

First focus on the case where \(n=0\), then \(n > 0\) and finally \(n < 0\).

Parameters

• x (float) – the base number \(x\).

• n (int) – the power \(n\).

Return type

float

Returns

the computed value.

Exercise 3.10: Ackermann function

Video 3.10: Exercise walkthrough

Now, you will implement the Ackermann function using recursion.

The Ackermann function, \(A(m, n)\), is defined as:

\[\begin{split}A(m, n) = \begin{cases} n+1 & \text{if } m = 0 \\\\ A(m-1, 1) & \text{if } m > 0 \text{ and } n = 0 \\\\ A(m-1, A(m, n-1)) & \text{if } m > 0 \text{ and } n > 0 \end{cases}\end{split}\]

Try the following examples to see if your solution is correct:

>>> print("A(3,4) =", ackermann(3, 4))
A(3,4) = 125
>>> print("A(2,5) =", ackermann(2, 5))
A(2,5) = 13

Add your function to the file cp/ex03/ackermann.py to test your solution.

cp.ex03.ackermann.ackermann(m, n)

Compute the Ackermann’s function \(A(m, n)\).

Your implementation should use recursion and not loops.

Parameters

• m (int) – the variable m.

• n (int) – the variable n.

Returns

the computed value \(A(m,n)\).

Note

The following exercises are part of Project 2: Strings and basic iterations. The link contains additional details, including how to hand in your results.

Exercise 3.11: The bisection algorithm.

Video 3 project work: Get started and use tests to solve your problems

Consider a function \(f\) so that \(f(x)\) is well-defined for all real numbers \(x \in \mathbb{R}\). One of the most important tasks in engineering is to find the roots of \(f\). Recall that a root is a value of \(x\) such that

\[f(x) = 0\]

In some cases, we can compute the roots explicitly. For instance, if \(f(x) = 2x^2 - 8\), you can easily check that \(x = 2\) and \(x=-2\) are both roots. However, in general roots can be difficult to find with an explicit formula, and therefore we will try to solve the problem numerically using the bisection method. To make the problem concrete, we will from now on assume \(f\) is the following function:

(1)\[f(x) = \sin\left( 3 \cos\left( \frac{x^2}{2} \right) \right)\]

You can find a plot of \(f\) below.

(png, hires.png, pdf)

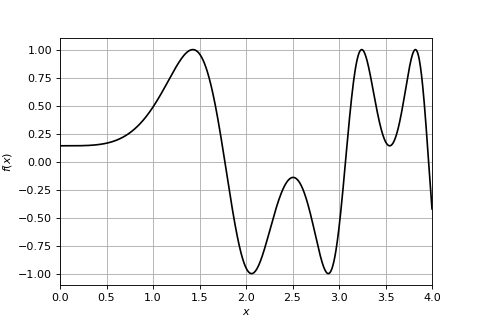
Plot of the function we wish to find roots of. The function has infinitely many roots.

As a warmup, implement the function defined in (1) as f().

For testing and handing in your function put in the file cp/ex03/bisect.py.

cp.ex03.bisect.f(x)

Find the roots of this function.

You should implement the function f(x) here.

Parameters

x (float) – The value to evaluate the function in x

Return type

float

Returns

f(x)

Exercise 3.12: Concluding there is a root

The bisection algorithm assumes that the function \(f\) is continuous, that is, the curve can be drawn as a single line without lifting the pen from the paper so to speak. Clearly our choice of \(f\) is continuous.

If a function is continuous, then if we select two points numbers \(a\) and \(b\) (we assume \(a \leq b\)), then we can conclude there must be a root in the interval \([a, b]\) if one of the following two conditions are met:

Note

To understand the last condition, if \(f(a) > 0\) and \(f(b) < 0\), clearly the curve of \(f\) must cross the \(x\)-axis, and hence it must have a root.

• Either \(a\) or \(b\) are themselves a root (i.e. \(f(a) = 0\) or \(f(b) = 0\))

• The values \(f(a)\) and \(f(b)\) are on opposite sides of the \(x\)-axis

The figure below we have illustrated two examples. In the first (blue) example \(a=1, b=2\) and we can conclude there must be a root. In the second example (red) \(a=3.2, b=3.8\) and the criteria indicate there is no root. Your jobs is to complete the function cp.ex03.bisect.is_there_a_root() which, given an \(a\) and \(b\), return True when the criteria is met and otherwise False.

(png, hires.png, pdf)

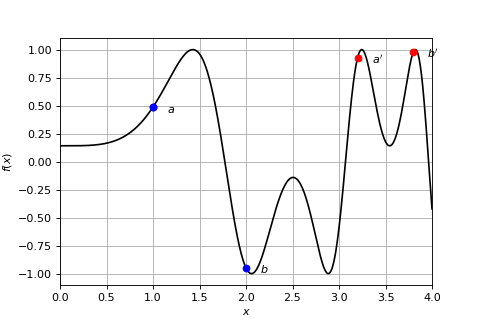
Examples of intervals where we can, and cannot, conclude the function has a root.

Here is an example of how you might use the function

>>> is_there_a_root(1, 2) # yes
True
>>> is_there_a_root(3.2, 3.8) # no
False
>>> is_there_a_root(1, 3.5) # actually there is a root, but the method here does not know it.
False

Warning

You might have noticed that the criteria may well be False even if there is a root in the interval \([a, b]\), for instance if \(a=1, b=3.5\). This is the expected behavior of the function.

To check your function with the supplied tests and to be able to hand it in, add it to the same file as in the previous exercise (cp/ex03/bisect.py).

cp.ex03.bisect.is_there_a_root(a, b)

Return True if we are guaranteed there is a root of f in the interval \([a, b]\).

Parameters

• a (float) – Lowest x-value to consider

• b (float) – Highest x-value to consider

Return type

bool

Returns

True if we are guaranteed there is a root otherwise False.

Exercise 3.13: Bisection

(png, hires.png, pdf)

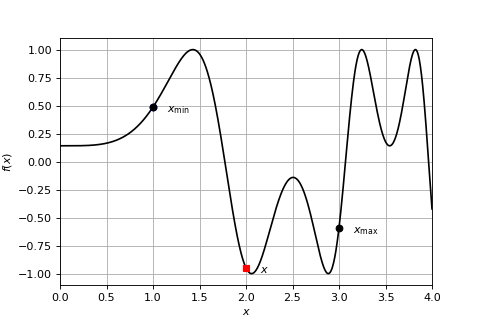
First step of the bisection method

We are now ready to discuss the bisection algorithm. Consider the above figure and suppose we are given two values \(x_{\min}\) and \(x_{\max}\) so that \(x_{\min} \leq x_{\max}\) and they are on opposite sides of the \(x\)-axis (i.e., they satisfy the criteria above). Next, suppose we select the mid-point between the two points, \(x = \frac{ x_\min + x_\max }{2}\). For instance, in the figure \(x_\min = 1, x_\max = 3\) and \(x=2\).

It should be clear that at least one of the intervals \([x_\min, x]\) (left) and \([x, x_\max]\) (right) must satisfy the condition checked by is_there_a_root() and hence must contain a root. We can now repeat the procedure on the interval that satisfy the criteria and select a new \(x\). In the above example, it will be the left-most interval, and the new step, along with the new \(x = 1.5\), is indicated in the figure below:

(png, hires.png, pdf)

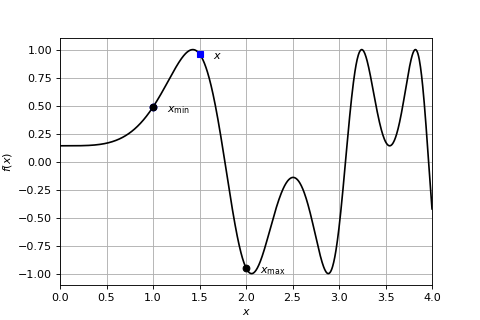
Second step of the bisection method.

Note

It is very common for numerical algorithms to contain terms such as \(\delta\). If you think about it, \(\delta\) represents a trade-off in computational speed and accuracy of the algorithm. This is a very common theme in numerical analysis!

Clearly in each step, the intervals become smaller and smaller, and hence we can select a tolerance \(\delta\) (for instance, \(\delta = 0.1\)) and at the first step where

(2)\[x_{\max} - x_{\min} \leq 2\delta,\]

we can compute the mid-point \(x\) anew and conclude there must be a root \(f(x^*) = 0\) so that \(|x^* - x| \leq \delta\) – at this point \(x\) is good enough and we can return \(x\).

The method you implement in the function bisect() should therefore do the following:

• It is given two values \(x_{\min}\) and \(x_{\max}\) so that \(x_{\min} \leq x_{\max}\) and a tolerance \(\delta\)

• It checks if the tolerance condition in (2) is met and if so return the midpoint \(x\)

• Otherwise, it computes \(x\), and check if the left-hand split must contain a zero according to the criteria in is_there_a_root()

  • If so, it (recursively) evaluates itself on the left-hand root

  • Otherwise, it (recursively) evaluates itself on the right-hand root

• To prevent infinite recursion, if \(x_\min\) and \(x_\max\) does not satisfy the condition in is_there_a_root() it should return the special value math.nan:

To check your function with the supplied tests and to be able to hand it in, add it to the same file as in the previous exercise (cp/ex03/bisect.py).

>>> bisect(1, 3, 0.01) # Compare to the figure
1.7734375
>>> bisect(1, 3, 0.2) # Much higher tolerance
1.875
>>> bisect(1, 3.5, 0.01) # return math.nan to avoid a potential infinite recursion
nan

cp.ex03.bisect.bisect(xmin, xmax, delta)

Find a candidate root within xmin and xmax within the given tolerance.

Parameters

• xmin (float) – The minimum x-value to consider

• xmax (float) – The maximum x-value to consider

• delta (float) – The tolerance.

Return type

float

Returns

The first value \(x\) which is within delta distance of a root according to the bisection algorithm